For probabilities, use Fermi numbers, not words
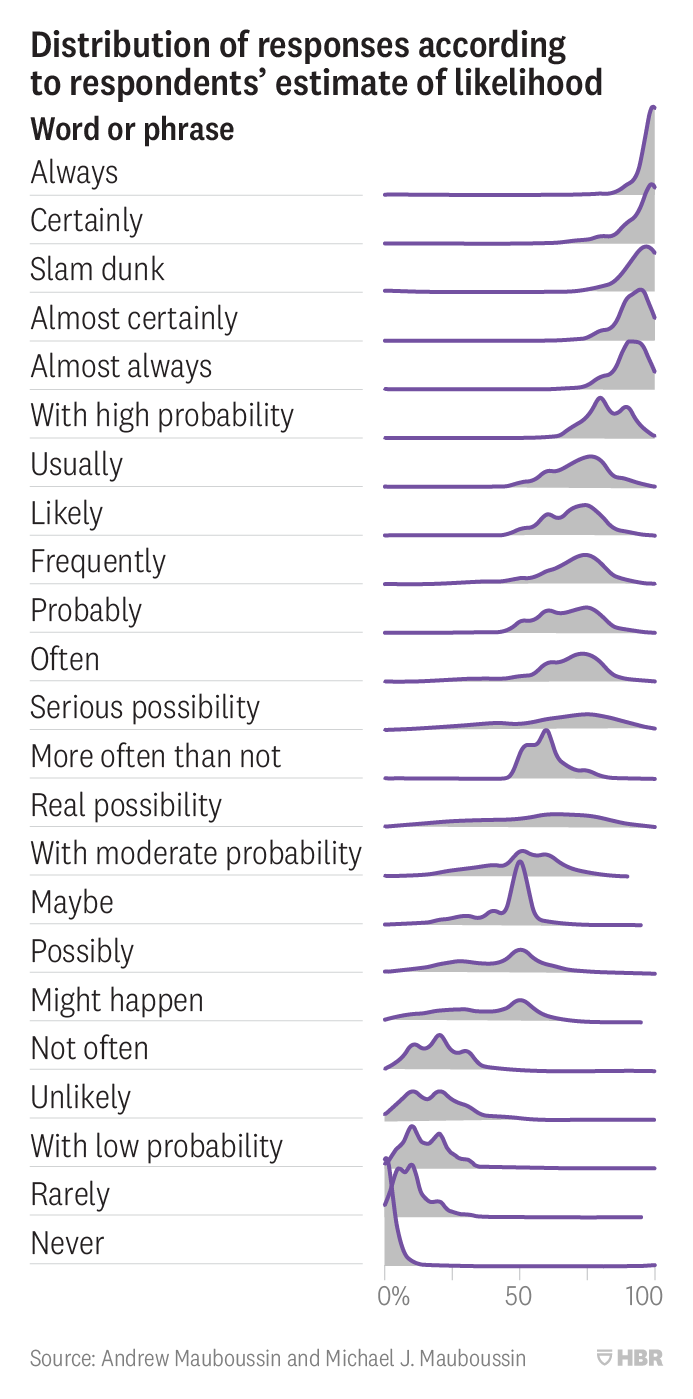
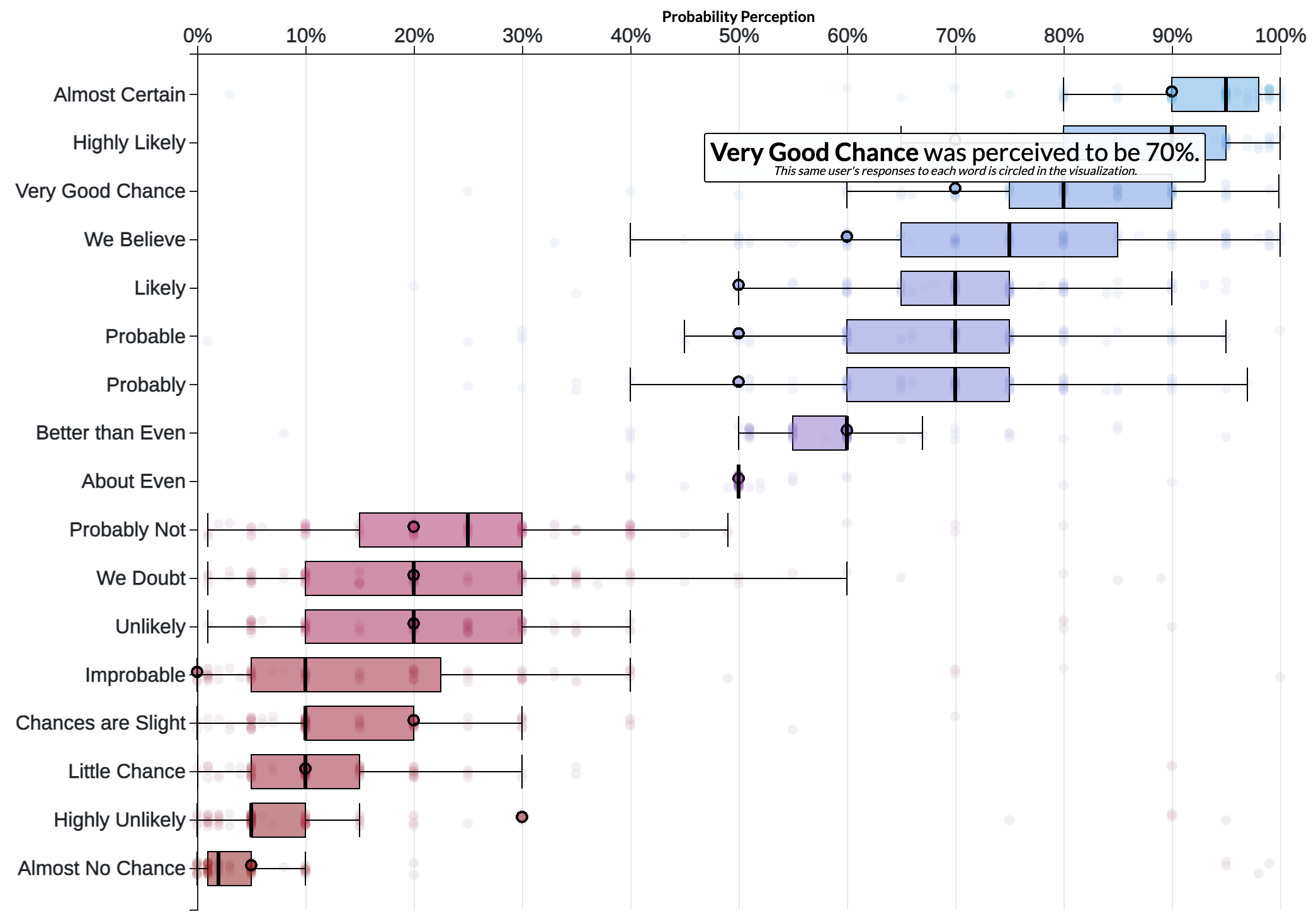
Figure 1: Study: Distribution of numeric probabilities implied by probability-words
Probability words
Words have fuzzy meanings (Figure 1), but that alone doesn’t mean words are useless.
However, we find serious problems when we examine these words in more detail. Another study gives us even more insight:
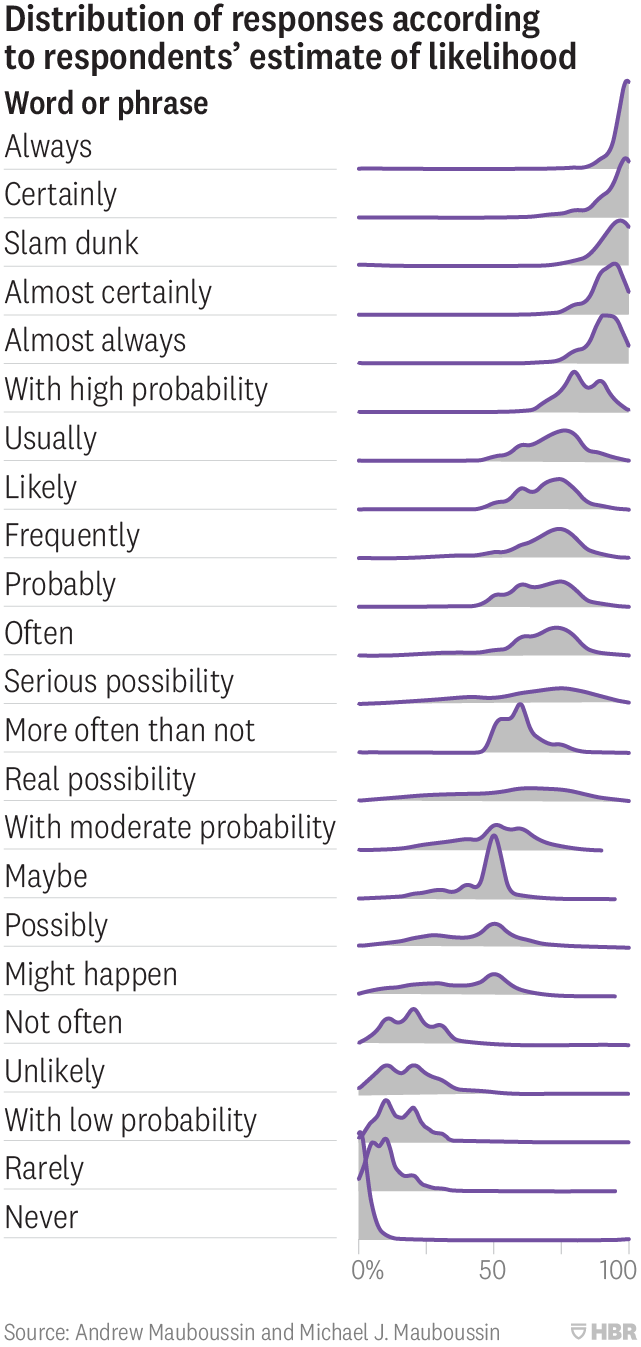
Figure 2
Note that the median intended probability of the word “likely” is 70%, whereas the intention of “unlikely” is 20%. Since that is the same word, just negated, we should expect the numbers to be symmetric like 70/30 or 80/20, but instead we’re biased.1
Even worse with “probable / improbable” at 70/10, and strangely while “probable” and “probably” are the same at 70%, “probably not” is 25% while “improbable” is 10%. Perhaps that makes sense to a grammatician, but surely this causes confusion in normal people, especially when we’re applying these words in analytical contexts like risk-analysis or debating a strategy.
1 There is extensive literature on our innate bias regarding both rare and common events; people are surprised how often 5% things happen, and how often 95% don’t. Nassim Taleb’s Black Swan expounds on this, and it’s obvious in our everyday experience, like how we get upset when a “10% chance of rain” rains out our picnic.
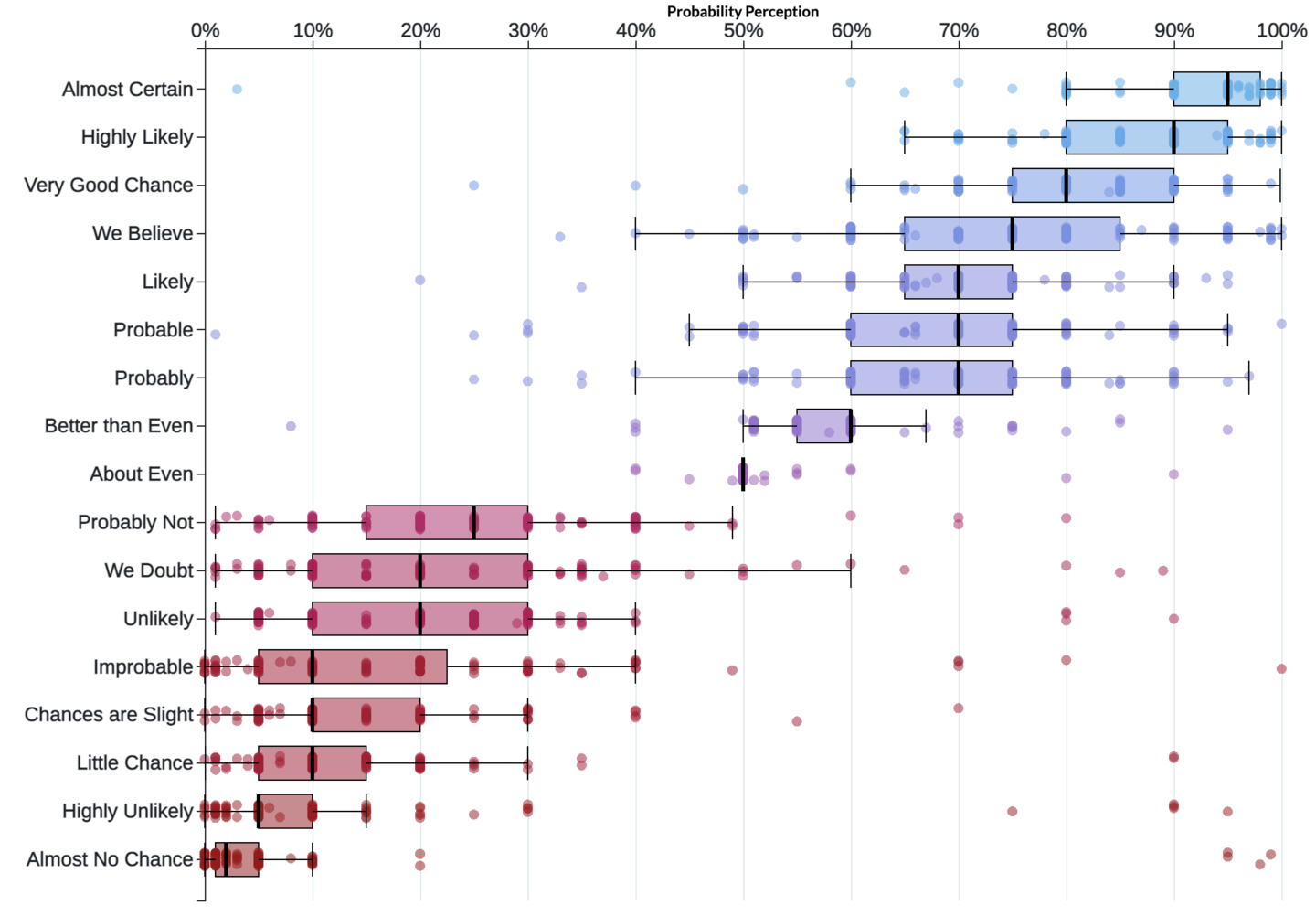
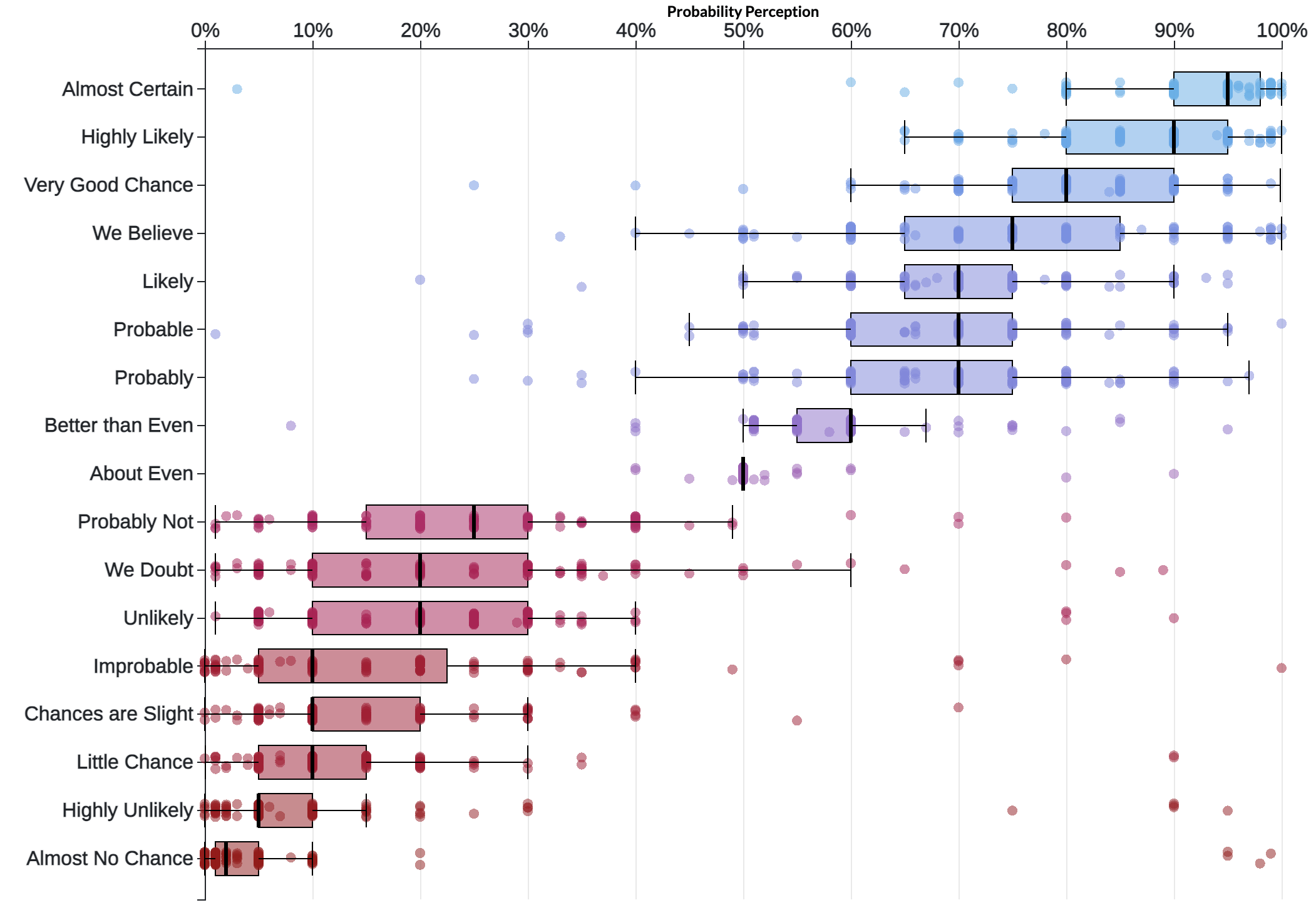
The communication problem is even worse because individual people disagree to an even larger extent. For example, these dots are a single person’s evaluation for these words:
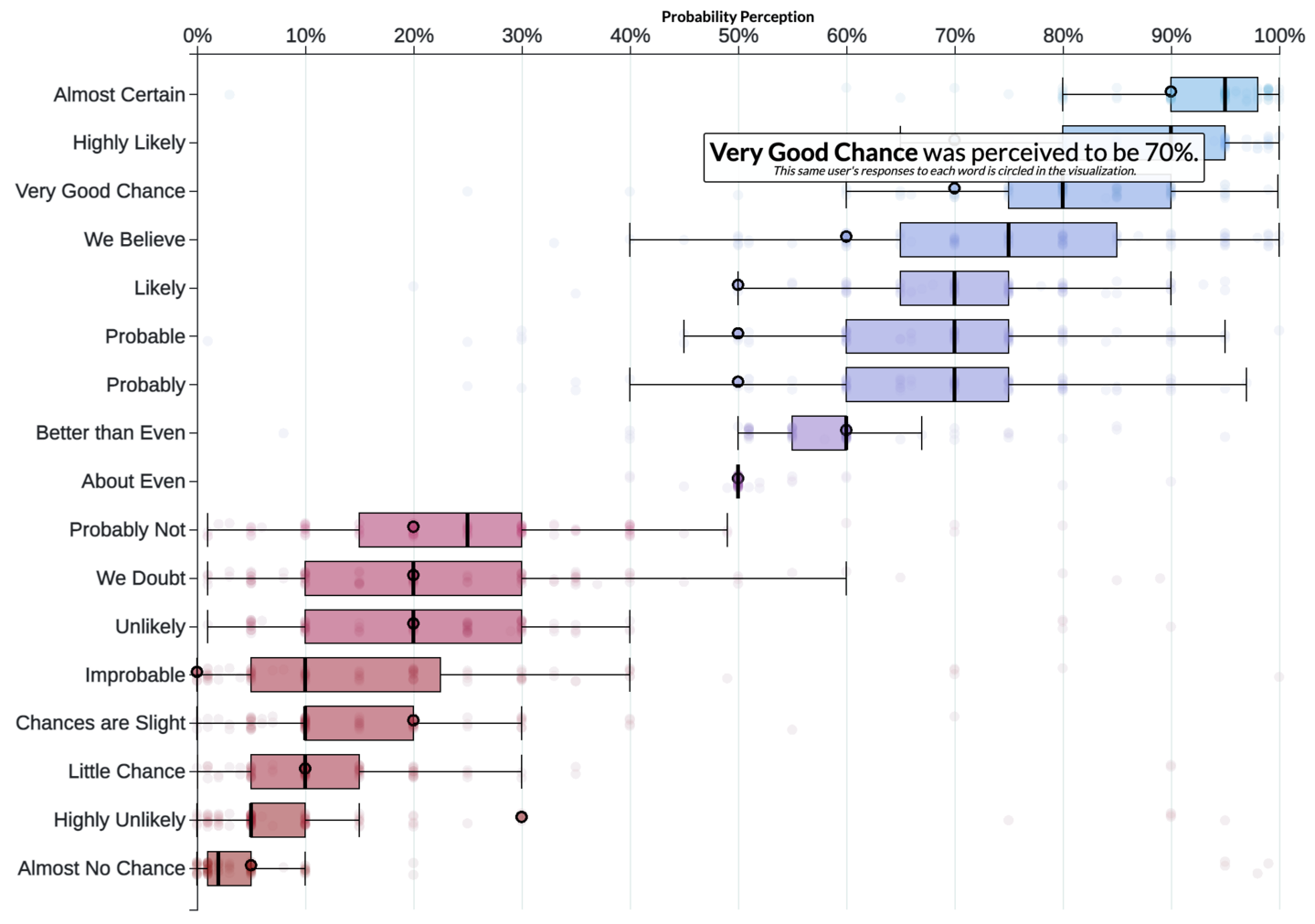
Figure 3
Note how pessimistic they are on the positive words, scoring “probable,” “probably,” and “likely” as only 50%. Then matching the median of 20% with their negatives (“probably not,” “we doubt,” “unlikely”), but then they claim “improbable” is a straight-up 0% while “highly unlikely” is still 30%.
I feel for this person. Although I admit the formal definition of “improbable” cannot be exactly 0%, what do I think in real life? If the consensus is that some project is “improbable” to complete on-time, I would certainly act as though that probability were 0%.
So that’s the point: Words don’t work, because the differences between individual interpretations are larger than the differences between the words themselves!
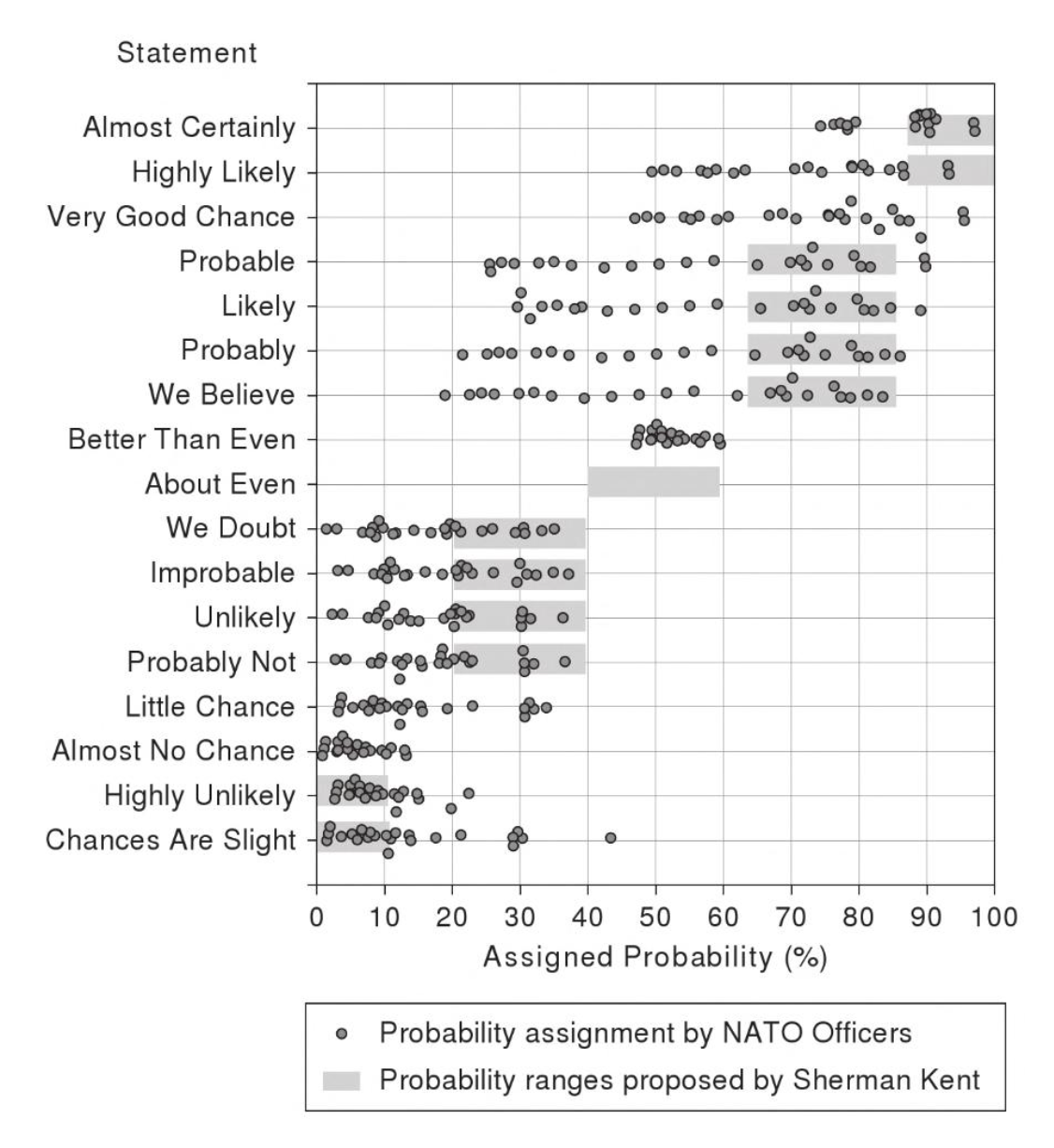
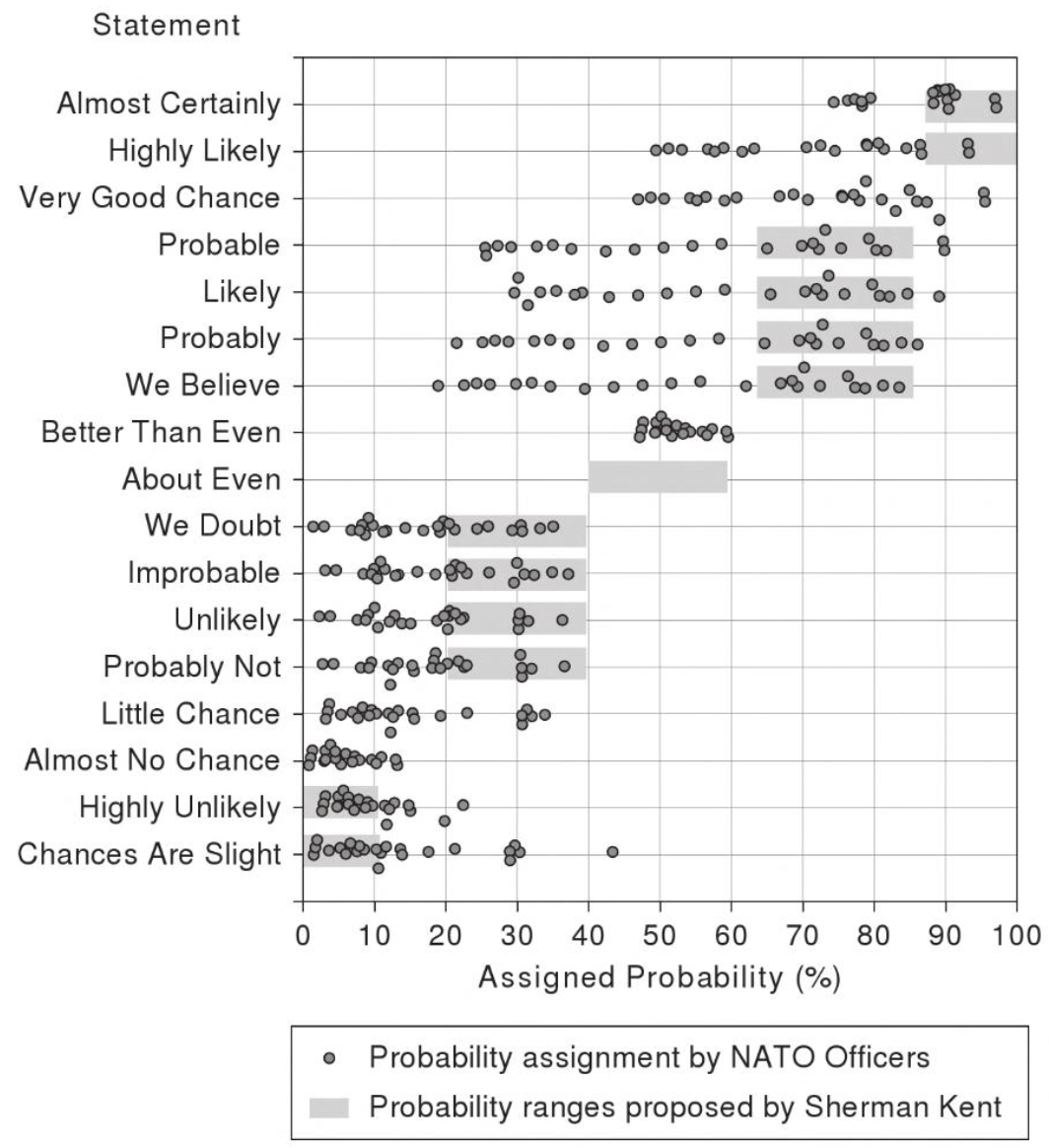
Furthermore, even if you assign an official numeric probability to words, and train competent people to adhere to those definitions, it still doesn’t work. The CIA attempted exactly this, publishing what they call the “Sherman Kent Scale.” It explains, for example, that “probable” is defined as 75% and “almost certainly not” is defined as 7%. However, when officers were assessed against the scale, fully half the time they failed to stay in-range (the grey bars):
Figure 4: “Clearly, the readers in this experiment were not using the Sherman Kent scale even though they were familiar with it.” —Scott Barclay, author of this study
We should give up on using words to describe probabilities.
The solution: Specific probabilities, Fermi-style
An obvious solution is to force people to use numeric probabilities, never2 using vague words. Indeed, this one rule will already improve communication.
2 Oops, I mean 0.2% of the time.
But writing down precise probabilities is hard.
It’s hard because usually3 we cannot specify the probability with precision. The world is often4 unpredictable even with expertise and data, so we need fuzzy ranges of probability to gesture towards our intent.
3 Oops, I mean 83.6% of the time.
4 Oops, I mean 62.9% of the time.
In this sense, it could appear more accurate to say “the project is unlikely to succeed” exactly because it’s unknown whether the true probability is 10% or 40%. Still, given individual interpretations of the word “unlikely,” we’re not accurately communicating that range.
Furthermore, as we know from Fermi Estimation in domains like “impact” and “time estimation,” it’s unproductive to haggle over details like “is it a 20% or 30% probability.” None of us likely5 knows the true number, and anyway we need crisp signals to make smart decisions.
5 Oops, I mean 9.1% of the time.
Therefore, the solution is a Fermi-style probability:
- Use numbers, not words.
- Select from a small set of options.
This is the same conclusion the CIA came to in the above-referenced 1964 study. Their mistake was to continue using words, but their categorical probabilities were Fermi:
| Probability Word | Probability Value | Expected Range |
|---|---|---|
| Certain | 100% | 100% |
| Almost Certain | 93% | 87% … 99% |
| Probable | 75% | 63% … 87% |
| Chances About Even | 50% | 40% … 60% |
| Probably Not | 30% | 20% … 40% |
| Almost Certainly Not | 7% | 2% … 12% |
| Impossible | 0% | 0% |
My recommendation is to use just a few raw numbers, without words, with instructions for “rounding off” that depend on the context.
For example, in estimating the likelihood that a project completes on time, we know that in general things are more likely6 to be late than early, therefore we should “round off” towards the lower probability.
6 Oops, I mean more than 51% of the time.
So go to your “risk” slides, and use Fermi probabilities to force yourself to decide what you think the risk really is, so everyone can decide whether or not to act.
Go to your strategy, and put Fermi probabilities on each assertion, so people know what is more or less likely to change as we learn and grow.
Go to your work-prioritization system, and put Fermi probabilities on the “value” or “estimate” metrics that you’re using for decision-support. Ask everyone in the team to supply their own numbers independently; where there’s disagreement, that’s worth a discussion; where there’s agreement, you can save time by just moving along. Or maybe don’t, because you realize that probability isn’t even applicable to such things.
Perhaps the real reason we use wishy-washy probability words is because we really don’t know the probability, and rather than admitting that, we just glide past the challenge. That’s the worst reason of all.
Now you have no excuse.
Be brave, and put a number on it.
https://longform.asmartbear.com/probability-words/
© 2007-2025 Jason Cohen
 @asmartbear
@asmartbear Simple eReader (Kindle)
Simple eReader (Kindle)
 Rich eReader (Apple)
Rich eReader (Apple)
 Printable PDF
Printable PDF